Against Mathiness

Principles for effective use of math in policy research, Part 1

As you can see, members of Congress, this complicated mathematical analysis supports my preferred policies.

This is Part 1, for Part 2 … head here.

Last November, I had the privilege of speaking at UCLA in the Jacob Marschak Interdisciplinary Colloquium on Mathematics in the Behavioral Sciences. My lecture was titled “Mathiness where Science Meets Politics,” and I provided a tour of research that I’ve been involved in over the past 30 years that has — for better or worse — made its way into highly contested settings where science, policy and politics collide.

“Mathiness” is a term coined by economist Paul Romer, who characterized it as a style that “lets academic politics masquerade as science.” Romer explains:

[M]athiness uses a mixture of words and symbols, but instead of making tight links, it leaves ample room for slippage between statements in natural versus formal language and between statements with theoretical as opposed to empirical content.

Romer’s “mathiness” is a play on comedian Stephen Colbert’s popularization of the idea of “truthiness,” which he characterized as:

“We're not talking about truth, we're talking about something that seems like truth – the truth we want to exist.”

Mathiness is the academic’s truthiness. Math makes research seem serious and science-like. For many consumers of research, math creates a barrier of technical sophistication that prevents the evaluation of truth-claims. When that happens, mathiness provides an aura of authority that says, “trust us, not them.”

In my UCLA talk, I opened by sharing that more than thirty years ago NASA called me up and asked me to retract my Master’s thesis, which was a comprehensive policy evaluation of the Space Shuttle program.

Awkward.

My 1992 Master’s thesis was adapted into a book chapter (PDF) in collaboration with my mentor Rad Byerly (RIP). We were the first to estimate to full costs of the Space Shuttle program, based on my explorations deep into NASA’s annual budgets, and it turns out those costs were much higher than NASA’s official costs.

Before coming to Colorado, Rad Byerly had been chief of staff of the House of Representative’s Space Subcommittee (where he oversaw the Congressional investigation into the Challenger accident) and then later, chief of staff of the House Science, Space, and Technology Committee — Rad was a big deal, so when something was published with his name on it, people noticed.

That landed our Space Shuttle cost estimates in The New York Times (see above) on March 22, 1993 — in 1992 dollars we estimated that the shuttle cost about $1.1 billion per launch, or $1.7 billion if we included development costs. That was 3-4x times higher than the costs that NASA represented to Congress.

Uh-oh.

So on the same day as the NYT article was published an official from NASA called me up in the graduate student bullpen where I had a desk. I remember it like it was yesterday. I thought initially, naively, he might be calling to congratulate me for the good policy work. He was not.

Instead, he said that NASA was concerned about our numbers and the political impact that they might have, as they differed so much from NASA’s “official” estimates. He requested that I issue a statement (or something like that) to call into question the accuracy of our estimates. I replied that the numbers are accurate, and besides, they are part of my 1992 Master’s thesis!

For me, it was an initial lesson in the fact that numbers carry with them political significance, which can be quite removed from the accuracy of those numbers or their connection to the real world. For some, the merit of policy research lies solely in its political expediency, and not in its truth value.

For NASA, it was obviously important at the time to convey to Congress that the Shuttle was good value for public money. That meant providing a plausibly defensible but lowball estimate of per-launch costs. When our numbers found their way into the New York Times, this created a political problem for NASA. It was a valuable lesson for me to learn, as I’ve see the dynamics repeated many times over my career.

This story has a surprisingly happy ending. In 2011, as the Space Shuttle program was wrapping up, Nature asked me to provide a comprehensive accounting of the program’s total costs, using the methods and updated data from our work back in the 1990s.

The 1971-2011 Space Shuttle program cost $279 billion overall in 2024 dollars.

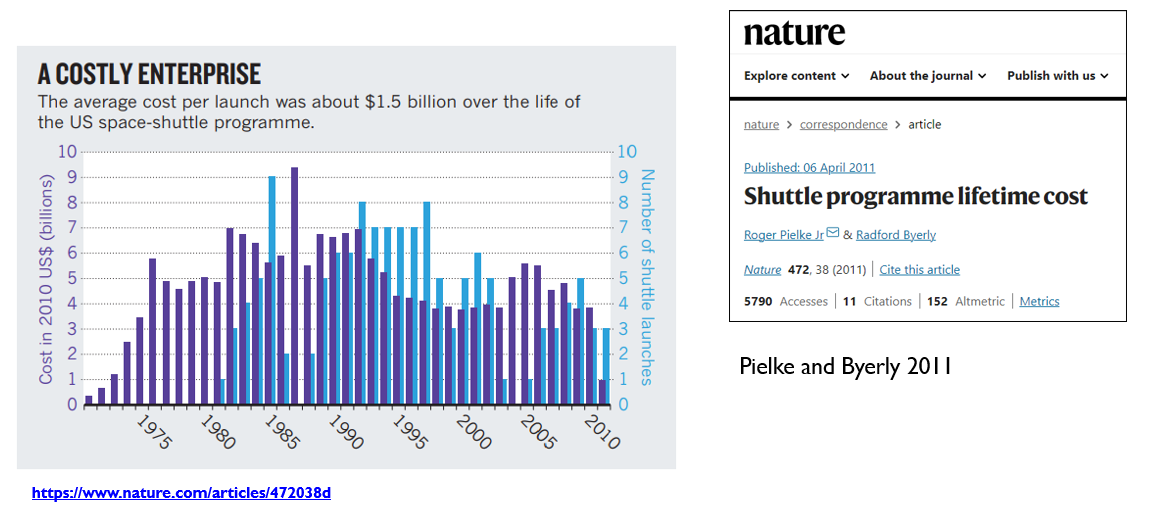
That final accounting, shown above, is widely accepted as the actual costs of the program, and now that Shuttle politics are ancient history, these numbers are even accepted by NASA. A lesson I took from this experience spanning several decades is that good empirical research can in fact win out in our truth battles, but it just might take some time — a long time in some cases.

Of note, in our 1992 paper, we projected how much the Space Shuttle program would ultimately cost per launch over the next several decades. Our projection turned out to be spot on, which you can see below.

Our 1992 projections of Shuttle program costs-per-flight for 2010. The red star indicates the actual costs-per-flight estimated in 2011. Not bad!

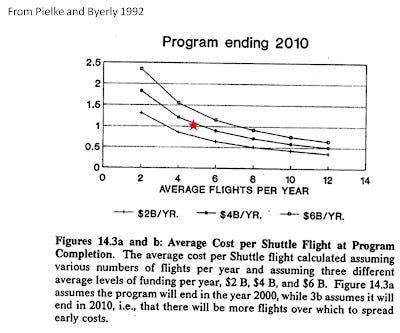
Another lesson: doing good policy research is possible, and it is also possible to tell the difference between that and mathiness, even if politics makes that difficult to see in the moment. It is easy to be seduced by mathiness and all the professional benefits that might come along with it, especially for highly partisan researchers. Similarly, there can be significant disincentives to doing good policy research if that research becomes politicized (especially by the “wrong” side).

In my UCLA talk, I went through a series of anecdotes like the Shuttle example from my experiences, and I suggested 10 principles for the effective use of math in policy research, based on seeing my work variously used and misused, celebrated and denigrated in policy settings as varied space policy, climate policy and sports governance. The 10 principles are a starting point for discussion.

Part 2 of this post discusses these 10 principles and invite your discussion and critique. Then, we can etch them in stone and bring them down from the policy mountain!

Happy 2024! Thanks for reading and subscribing. This next year is going to be a great one here at THB. Stay tuned for details.